1.ダイオードのモデル
半導体デバイス(物理モデル)の中で最も簡単なダイオードのモデルを用いて、半導体の特性とデバイスモデルのパラメータがどのように関係しているか見ていきます。この他のデバイスモデルについては、若干の半導体物理やプロセス技術に関する知識を必要としますが、ダイオードモデルであれば半導体の教科書に載っている1次元モデルで理解することができます。
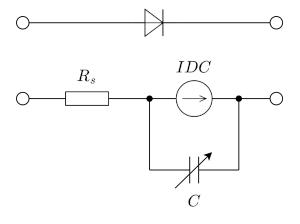
図1の\( \small IDC \)は、ダイオードの直流特性を表す非線型電流源です。\( \small Rs \)は、半導体バルク、オーミックコンタクトの接触抵抗などを含めた直列抵抗を表します。\( \small C \)は、キャリアの拡散容量と空乏層容量の和であり、バイアス電圧に依存します。この図より、直流特性は、\( \small IDC \) と \( \small Rs \)で決定され、交流特性は、\( \small Rs, C, dIDC/dV \)によって決定されることが解ります。過渡応答特性には、全てのデバイスモデルパラメータが関係します。さらに、デバイスモデルパラメータとしては定義されていませんが、 \( \small GMIN (単位 = \Omega^{-1}, デフォルト値 = 10^{-12}) \)の値のコンダクタンスが、自動的に \( \small IDC \)と並列に挿入されています。これは、.OPTIONS コマンドで値を設定できますが、SPICEの数値計算の収束安定性を確保するためのものなので、 \( \small GMIN = 10^{-12} \)よりは小さくできません。このパラメータは、逆方向の漏れ電流の直流バイアス依存性を表現するためにも利用可能です。
2.pn接合ダイオードのI-V特性
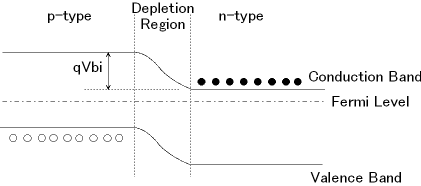
pn接合ダイオードのゼロバイアス状態(熱平衡状態)のバンド図を図2に示します。図2に示したp型とn型半導体の間の電位差\( \small Vbi \)は、ビルトイン・ポテンシャルと呼ばれ、p型半導体とn型半導体のキャリアの濃度差、即ちフェルミレベルの差による空乏層 (Depletion Region or Depletion Layer) の形成により生じます。この電位差によりn型半導体の多数キャリアである自由電子とp型半導体中の多数キャリアであるホールが空乏層によって塞き止められたような形となっています。
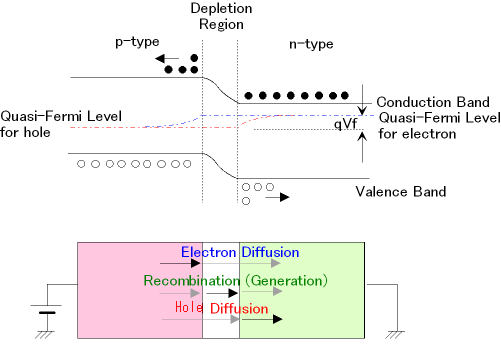
図3に順方向バイアス印可時のバンド図を示します。順方向バイアス\( \small V \)の印可によりビルトイン・ポテンシャル\( \small Vbi \) が\( \small Vbi – V \)に減少します。フェルミレベルは、本来、熱平衡状態でしか定義できませんが、接合面から離れた(電荷の)中性領域には、殆ど電圧がかからないため、中性領域だけに適用できるフェルミレベルが定義できます。この制限付きフェルミレベルは、Quasi-Fermi Level(擬フェルミレベルと訳している本もありますが、通常、クェーザイ・フェルミレベルと言う)と呼ばれ、n型半導体中とp型半導体では異なる値となります。従って、図3のように、空乏層と電荷が注入された空乏層付近の領域では、電子に対するQuasi-Fermi Level(青色)とホールに対するQuasi-Fermi Level(赤色)が分離することになります。このQuasi-Fermi Levelの分離の大きさが、少数キャリア濃度の平衡状態からのずれの大きさを表しており、これに基づいて注入レベル(熱平衡時より増えたキャリア量)の大きさを見積もることができます。注入レベルが小さく、多数キャリアの濃度変化が無視できる場合が低水準注入とよばれ、多数キャリア濃度の変化が無視できない場合が高水準注入と呼ばれます。高水準注入と低水準注入では、電流ー電圧特性の形が異なってきます。図3は、低水準注入の場合、即ち、少数キャリアの濃度勾配のみを考慮して描かれています(つまり、多数キャリアに対するQuasi-Fermi Levelが平坦です)。バンド図の中に、ホールと電子の濃度勾配による少数キャリアの拡散を示す矢印を描きました。これに対応する電流が、下の1次元pn接合モデルの中で、Electron DiffusionとHole Diffusionとして示してあります。これらの電流は、拡散電流と呼ばれ、この電流メカニズムに基づく電流-電圧特性を示すダイオードが理想ダイオードと呼ばれます。拡散電流は、主に半導体のバンドギャップまたは真性キャリア濃度\(\small n_i \)の大きさによって特徴づけられます。
さらに、同図には、Recombination (Generation) という矢印が描かれています。\(\small p \)をホール濃度、 \(\small n \)を自由電子濃度、 \(\small n_i \)を真性キャリア濃度とするとき、順方向バイアス条件下では、青いQuasi-Fermi Levelが上にくるため、空乏層内とその付近で、 \(\small pn > n_i^2 \)となり、再結合レートが熱平衡状態よりも大きくなります。逆に、逆方向バイアス条件では、赤いQuasi-Fermi Levelが上にくるため、\(\small pn < n_i^2 \)となり、熱的発生レートが熱平衡状態の場合よりも大きくなります。これらのキャリアの発生または再結合による電流が、発生・再結合電流または空乏層電流と呼ばれる電流成分です。これは、主に空乏層中で起こる現象なので、逆バイアスまたは小さな順方向バイアス条件下で顕著に表れます。
以上のように、ダイオードの直流電流-電圧特性は、拡散電流(低水準または高水準注入条件)、発生・再結合電流でモデル化できますが、この他に、雪崩降伏現象(逆方向ブレークダウン)と直列抵抗による電圧降下の影響が現れます。
拡散電流モデルは、通常、理想ダイオード特性として半導体デバイスの教科書に紹介されているものです。SPICEでは、次の式(1a), (1b) で表します。
[注] 以後、SPICEのモデルパラメータは、赤文字で示すことにします。
\begin{eqnarray}
I_D &=& \textcolor{red}{Is} (e^{\frac{qV}{kT}} – 1) \tag{1a} \\
\textcolor{red}{Is} &=& q S n_i^2 ( \frac{D_p}{L_p N_d} + \frac{D_n}{L_n N_a} ) \tag{1b}
\end{eqnarray}
ここで、\(\small \textcolor{red}{Is} \)は、飽和電流と呼ばれ、\(\small S \)は接合面積、\(\small n_i \)は真性キャリア濃度、\(\small D_p, D_n \)は、ホールと電子の拡散係数、\(\small L_p, L_n \)は、ホールと電子の拡散長、\(\small N_d, N_a \)は、ドナー濃度とアクセプタ濃度です。
一方、発生・再結合電流は、Shockley-Hall-Read 統計と呼ばれるキャリアの発生・再結合モデルに基づき、次のように求められます。
\begin{eqnarray}
I_{RG} &=& \textcolor{red}{Is} (e^{\frac{qV}{2kT}} – 1) \tag{2a} \\
\textcolor{red}{Is} &=& \frac{q S n_i W}{2 t_o} \tag{2b}
\end{eqnarray}
ここで、\(\small W \)は空乏層の幅、\(\small t_o \)は、発生・再結合レートです。\(\small I_D \)と\(\small I_{RG} \)では、\(\small Is \)の物理的意味が異なっていますが、これらをまとめて次のように表します。
\[ I_{DC} = \textcolor{red}{Is} (e^{\frac{qV}{ \textcolor{red}{N} kT}} – 1) \tag{3} \]
ここで、\(\small \textcolor{red}{N} \)は、Ideality Factor または、発生・再結合電流における Emission Coefficient と呼ばれる値です。\(\small I_{RG} \)と\(\small I_D \)の比率は、電圧によって変化するため、\(\small \textcolor{red}{N} \)の値も印可電圧に依存して変化しますが、オリジナルのSPICEモデルでは、\(\small \textcolor{red}{N} \)に一つの値しか与えることができません(現在のSPICE系シミュレータでは、\(\small \textcolor{red}{NR}, \textcolor{red}{ISR}\)で、Ideality Factor または、発生・再結合電流を設定可能)。
式(1b)のように、\(\small \textcolor{red}{Is} \)は、真性キャリア濃度\(\small n_i \)と関係しています。また、\(\small ni \)は、温度によって大きく変化します。そこで、SPICEでは、バンドギャップ\(\small EG \)と バンド端の実効状態密度に関する温度指数\(\small \textcolor{red}{XTI} \)を用いて、\(\small \textcolor{red}{Is} \)の温度変化をシミュレートします。また、指数関数内の計算式は、バンドギャップの温度依存性を級数展開して1次近似したものです。
\[ \frac{Is(T2)}{Is(T1)} = \bigg( \frac{T2}{T1} \bigg)^{ \frac{ \textcolor{red}{XTI} }{ \textcolor{red}{N}}} e^{ (\frac{-q \textcolor{red}{EG} }{ \textcolor{red}{N} kT2})(1 – \frac{T2}{T1}) } \tag{4} \]
pn接合では、\(\small \textcolor{red}{XTI} = 3, EG = 1.11eV @300K (Si), \textcolor{red}{EG} = 0.67eV @300K (Ge) \)です。拡散電流は、\(\small n_i^2 \)に比例、発生・再結合電流は、\(\small n_i \) に比例しますが、式(4)は両ケースに対応しています。
以上は、低水準注入の仮定に基づく解析ですが、オリジナルのSPICEには、高水準注入をシミュレートするパラメータが有りません(現在のSPICE系シミュレータでは、\(\small \textcolor{red}{IKF}\)で調整可能)。高水準注入の拡散電流は、\(\small \textcolor{red}{N} = 2 \)の特性となり、電流-電圧特性の傾きが小さくなるので、直列抵抗\(\small \textcolor{red}{Rs} \)による電流-電圧特性の傾きの鈍りを利用して、高水準注入の影響を模擬することが行われています(シミュレータによっては\(\small \textcolor{red}{N} \)の値をバイアス電圧によって変更可能)。実際の測定においても、直列抵抗の影響と高水準注入の影響を分けることは困難です。直列抵抗による電圧降下の影響を求めるためには、次の非線型方程式の数値解を得なければなりませんので、シミュレーションによって、\(\small \textcolor{red}{Rs} \)の値を調整します。
\[ I_{DC} = \textcolor{red}{Is} (e^{\frac{q (V – \textcolor{red}{Rs} I_{DC})}{ \textcolor{red}{N} kT}} – 1) \tag{5} \]
ダイオードモデルでは、逆方向のブレークダウンをシミュレートすることができます。バイポーラトランジスタでは、このパラメータがないので注意が必要です。ブレークダウンのシミュレーションでは、ブレークダウン開始電流\(\small \textcolor{red}{IBV} (\gt 0) \)とブレークダウン電圧\(\small \textcolor{red}{BV} (\gt 0) \)が用いられます。
\begin{eqnarray}
I_{DC} =
\begin{cases}
-\textcolor{red}{IBV} & (V = BV) \\
-\textcolor{red}{Is} (e^{ \frac{-q(\textcolor{red}{BV} + V)}{kT} } – 1 + \frac{q\textcolor{red}{BV}}{kT} ) & (V \lt -BV) \tag{6}
\end{cases}
\end{eqnarray}
式(6)は、雪崩降伏のモデルに基づいているので、拡散電流モデルとの接続には注意を要します。即ち、\(\small IBV = Is (qBV/kT) \)とすべきです。Zener ダイオードとショットキーダイオードのブレークダウン特性のモデリングについては、追加でパラメータの調整が必要です。また、ツェナー降伏の精密なマクロモデルや物理モデルが報告されていますが、ここでは省略します。
尚、SPICE ダイオードモデルには、雑音解析用にフリッカーノイズ (1/fノイズ) をシミュレートするためのパラメータもあります。半導体デバイスのフリッカーノイズは、主に、空乏層のキャリアトラップ(結晶欠陥や汚染不純物によりバンドギャップ中に生じた局在準位にキャリアが捕獲されること)によって発生することが知られています。この場合、単位周波数のノイズパワー密度(自乗平均)は、次のようになります。
\[ \overline{i_d^2} = 2q i_d df + \textcolor{red}{KF} i_d^{ \textcolor{red}{AF} } \frac{df}{f} \tag{7} \]
ここで、ノイズ電流\(\small i_d \)は、ダイオードに並列な電流源として表されています。\(\small \textcolor{red}{KF}, \textcolor{red}{AF} \)はそれぞれ、雑音係数、雑音指数と呼ばれています。
3.pn接合ダイオードのC-V特性
図2, 3 を比較すると、p型とn型の間のポテンシャル障壁が順方向バイアスにより低くなった分、空乏層の幅も短くなっています。このことは、印可電圧を変化させることにより、空乏層に貯えられる電荷量が変化することを意味しますので、交流信号に対してはキャパシタと等価であると考えることができます。但し、直流電圧により、空乏層が大幅に変化するので、キャパシタの容量は直流電圧の値に依存しています。
電磁気学によると、Qを電荷量、Vを導体間の電位差として、キャパシタの容量\(\small C \)は、
\[ C = \frac{Q}{V} \tag{8} \]
と定義されます。しかし、ダイオードの場合、\(\small C \)が定数ではなく直流電圧\(\small V \)に依存しますので、次のような小さな電圧の変化\(\small dV \)に対する電荷の微少変化\(\small dQ\)によって、次のように表すことにします。
\[ C(V) = \frac{dQ}{dV} \tag{9} \]
これは通常、空乏層容量\(\small C_j \)と呼ばれています。さらに、順方向バイアス印可時には、注入された少数キャリアもキャパシタに溜まった電荷として働くため、この効果も考慮しなければなりません。この注入キャリアによる容量成分を、拡散容量\(\small C_d \)と呼びます。従って、pn接合容量\(\small C \)は、次のように、\(\small C_j \)と\(\small C_d \)の並列接続で表現されます。
\[ C = C_d + C_j \tag{10} \]
空乏層容量の容量-電圧特性は、半導体中のドナーとアクセプタの濃度分布に依存しています。典型的な例として半導体デバイス工学の教科書で紹介されている階段接合と傾斜接合を仮定し、空乏層内の電荷分布からポアソンの方程式を解くと、次のような式が得られます。
(a) 階段接合
\[ C_{j1} = S \bigg( q \epsilon \frac{N_a N_d}{N_a + N_d} \frac{1}{ \textcolor{red}{Vj} \ – V} \bigg)^{ \frac{1}{2} } = C_{j1}(V = 0) \bigg(1 – \frac{V}{ \textcolor{red}{Vj} } \bigg)^{- \frac{1}{2}} \tag{11a} \]
(b) 傾斜接合
\[ C_{j2} = S \bigg( \frac{ q a \epsilon^2 }{12} \frac{1}{ \textcolor{red}{Vj} \ – V} \bigg)^{ \frac{1}{3} } = C_{j2}(V = 0) \bigg(1 – \frac{V}{ \textcolor{red}{Vj} } \bigg)^{- \frac{1}{3}} \tag{11b} \]
ここで、\(\small \epsilon \)は、半導体の誘電率、\(\small \textcolor{red}{Vj} \)は、ビルトイン・ポテンシャル(図2における\(\small V_{bi} \))、\(\small a \)は、傾斜接合の不純物濃度の接合面付近の勾配を表します。これらの式をひとまとめにすると、次のようになります。
\[ C_{j} = \textcolor{red}{Cjo} \bigg(1 – \frac{V}{ \textcolor{red}{Vj} } \bigg)^{- \textcolor{red}{m}} \tag{12} \]
ここで、\(\small \textcolor{red}{Cjo} \)は、ゼロバイアスにおける空乏層容量です。\(\small \textcolor{red}{m} \)は、階段接合(\(\small \textcolor{red}{m} = 1/2 \))または傾斜接合(\(\small \textcolor{red}{m} = 1/3\))を表しますが、実際のダイオードでは、この両極端のケースの間の値 (\(\small \textcolor{red}{m} = 1/2 \sim 1/3 \)) をとることになります。この空乏層近似による解析式は、\(\small V \lt Vj \) に於いて実測値と極めて良い一致を示すことが知られていますが、空乏層近似の成立しない順方向バイアス条件で数値計算上困った問題を起こします。即ち、\(\small V = Vj \) において \(\small C_j \)が無限大に発散してしまうということです。これを避けるために、SPICEでは、\(\small V = Vj \) に近づいたところで、\(\small C_j – V \) 特性を線形に外挿近似するようになっています。定義式は省略しますが、この近似の程度は、ポアソンの方程式を解く際に空乏層電荷の積分範囲を調整するパラメータ\(\small \textcolor{red}{FC} \)によって調整可能です。\(\small \textcolor{red}{FC} = 0 \)で、外挿が \(\small V = 0 \) から始まり、\(\small \textcolor{red}{FC} = 1 \)で外挿が \(\small V = Vj \) から始まる(即ち無限大に発散する)ようになっているので、\(\small V = 0 (V) \)付近での実測値と誤差が出ないようにします。
拡散容量\(\small Cd \)は、pn接合への印可電圧に対する少数キャリア濃度の応答の遅れによって見かけ上生じるものです。順方向バイアス印可されたpn接合の主要な容量成分であり、バイポーラトランジスタの動作周波数を決定する主要因でもあります。これは、蓄積電荷モデルの考え方に基づき電流-電圧特性から直接算出できます。
\[ C_{d} = \frac{dQ_D}{dV} = \textcolor{red}{TT} \frac{dI_D}{dV} \tag{13} \]
ここで、\(\small dQ_D \)は、電圧変化\(\small dV \)に対する、注入された電荷の変化であり、\(\small dI_D \)は、\(\small dV \)に対する拡散電流の変化です。\(\small \textcolor{red}{TT} \)は、トランジット時間と呼ばれるパラメータで、キャリアのライフタイムと拡散係数に関係しています。
以上のモデルパラメータをまとめると次の表のようになります。
| パラメータ | 意味 | デフォルト値 | 単位 | 備考 |
|---|---|---|---|---|
| Is | 飽和電流 | \( 10^{-14} \) | A | 面積ファクタの影響有り |
| Rs | 直列抵抗 | 0 | \( \Omega \) | 面積ファクタの影響有り |
| N | エミッション係数 | 1 | ||
| TT | トランジット時間 | 0 | s | |
| Cjo | ゼロバイアス接合容量 | 0 | F | 面積ファクタの影響有り |
| Vj | ビルトイン・ポテンシャル | 1 | V | |
| m | 接合傾斜係数 | 0.5 | ||
| EG | バンドギャップまたはショットキー障壁 | 1.11 | eV | 1.11:Si, 0.69:SBD, 1.42:GaAs, 0.67:Ge |
| XTI | 飽和電流の温度指数 | 3.0 | 3.0:Si, 2.0:SBD | |
| KF | フリッカ雑音係数 | 0 | ||
| AF | フリッカ雑音指数 | 1 | ||
| FC | 順方向バイアス空乏層容量係数 | 0.5 | ||
| BV | 逆方向ブレークダウン電圧 | \( \infty \) | V | |
| IBV | 逆方向ブレークダウン開始電流 | \( 10^{-3} \) | A | |
| TNOM | パラメータ抽出(測定)温度 | 27 | \({}^\circ \)C |
4.ショットキーダイオードへの応用
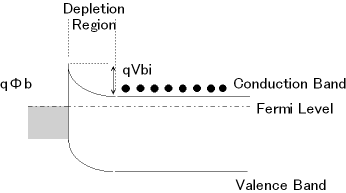
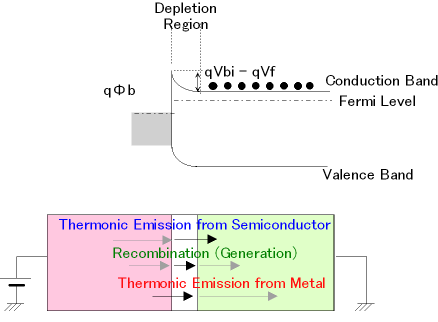
ショットキーバリア・ダイオードの特性は、半導体と金属のフェルミ準位の差により形成される電位障壁を乗りこえて流れる電流によって表せます。図4の熱平衡状態では、半導体側から金属への電子の流れと金属から半導体への電子の流れは釣り合っていますが、図5のように順方向バイアスを印可すると、同エネルギー状態の電子濃度の平衡が半導体と金属でずれてしまうため、半導体から金属への電子流が金属から半導体への電子流を上回るようになります。このメカニズムによる電流を熱放出電流 (Thermonic Emission Current) と呼びます。また、図5下図に示したように、pn接合の場合と同様、発生・再結合電流も流れます。さらに、半導体中のドナー濃度を高くし、空乏層幅が狭くなると、電子トンネリングによる電界放出 (Field Emission) が起こります。
熱放出電流は、次式で表されます。
\begin{eqnarray}
I_T &=& \textcolor{red}{Is} (e^{\frac{qV}{ \textcolor{red}{N} kT}} – 1) \tag{14a} \\
\textcolor{red}{Is} &=& S A^* T^2 e^{\frac{qV_{bs}}{kT}} \tag{14b}
\end{eqnarray}
ここで、\( A^* \)は、有効リチャードソン定数と呼ばれるもので、電子の有効質量から算出できます ( \(\small e.g. n-type Si : 250A/K^2, n-type GaAs : 8.1A/K^2 \) )。\(\small V_{bs} \)は、ショットキバリアの高さ(金属のフェルミレベルと半導体の電子親和力の差)です。従って、式(15a)のように、pn接合の電流-電圧特性と同形ではありますが、\(\small \textcolor{red}{Is} \)の温度依存性が pn接合とは異なることが解ります。即ち、pn接合のバンドギャップ\(\small EG \)をショットキバリアの高さ(金属側から見た高さ)で置き換えればよいということです。また、飽和電流温度指数\(\small XTI \)を 3.0 から 2.0 に変更すればよいということです。
容量-電圧特性に関しては、通常、半導体中の不純物濃度は均一として接合傾斜係数を \(\small \textcolor{red}{m} = 1/2 \)とします。また、ビルトイン・ポテンシャル\(\small VJ \)は、n型半導体の場合、次式で与えられます。
\[ \textcolor{red}{Vj} = q V_{bs} – \frac{kT}{q} ln \bigg( \frac{N_d}{n_i} \bigg) \tag{15} \]
ショトキーダイオードのその他の特徴として、多数キャリアの熱放出が主な電流となるため、少数キャリアの蓄積効果が生じないことがあげられます。このため、拡散容量が発生せず極めて高速な過渡電流応答を示す。従って、トランジットタイムが\( \textcolor{red}{TT} = 0s \)となりますが、通常、実測に基づき小さな値が設定されているようです。
演習問題
電子回路シミュレーションにより、以下の特性を確認してください。
- バンドギャップ\(\small EG \)を0.3eVから2.2eVまで変化させると、電流-電圧特性がどのように変化するか調べよ。
- 温度を変えると電流-電圧特性と容量-電圧がどのように変化するか。温度は、.OPTIONS TEMP=100 のようにして指定できる。
- 10ns 程度の電圧パルスに対する電流の応答波形を調べよ。また、\(\small TT \)の値を変化させるとどのように応答がかわるか。
- \(\small Rs \)の値を変化させると電圧パルスに対する、電流の応答は変化するか。
- \(\small m \)の値を、1から2まで変化させ、容量-電圧特性が変化するか調べよ。\(\small C^{-2} – V \)プロットと\(\small C^{-3} – V \)プロットを行い、直線性も調べよ。
- 上の課題5の結果から、ビルトイン・ポテンシャルを求めよ。
- 順方向バイアスでの電流-電圧特性から、Is を求める方法を考え、\(\small Is \)の温度依存性を調べよ。
- \(\small Rs \)を変化させたとき、順方向電流-電圧特性はどのように変化するか。但し、順方向電流軸を常用対数目盛りでプロットすること。
- 自分で、ショットキダイオードのモデルを作成し、pn接合ダイオードの特性と比較せよ。立ち上がり電圧、Isの温度依存性は、どのように違うか。
- \(\small BV, IBV \)の値を変化させながら、ブレークダウン電圧と電流がどのように変化するか確かめよ。
- 温度を変えると\(\small BV \)の値は、どのように変化するか。また、この変化は、理論と合っているか。
