1.BJTの構造
バイポーラトランジスタ(BJT)のモデルは、1次元の簡略化された物理的モデルに幾つかの2次的効果やフィッティング用のパラメータを加えて作られています。半導体物性についてのバックグラウンドとしてはpn接合ダイオードの動作原理を理解している必要があります。npn と pnp の2種類のモデルがありますが、極性が異なる以外は全く同じですので、ここでは、npn トランジスタのみを解説します。また、図1 のように電圧と電流の極性を定義することにします。尚、このページでは、ノイズ特性などを除く基本的なパラメータのみを説明しますが、ここで出てくるパラメータで、十分にBJTの基本特性を表現することができます。
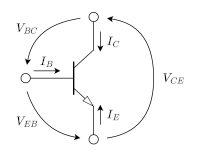
キルヒホッフの電流則と電圧則により、式(1a)、 (1b)が成り立ちます。
\begin{eqnarray}
I_E + I_B + I_C &=& 0 \tag{1a} \\
V_{EB} + V_{CE} + V_{BC} &=& 0 \tag{1b}
\end{eqnarray}
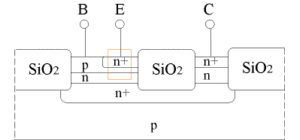
図2にBJTの断面構造の例を示します。SiO2層は、素子分離のために必要です。また、SiO2層下部に広がるn+層(高濃度のn型不純物を含む埋め込み層)は、コレクタ電流がコレクタ電極に届くまでの抵抗値を下げるために挿入されています。どのようにしてこのような構造を作ることができるのか興味がある人は、プロセス-デバイスシミュレータのページを見てください。SPICEでは、この構造を1次元で近似します。図中に柿色で囲った”n+/p/n”の部分が1次元モデルで表現される部分です。
2.Ebers-Moll のモデル
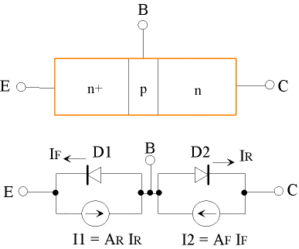
SPICEでは、BJTの直流特性を示すために Ebers-Moll のモデルまたは Gummel-Poon のモデルを使用します。Gummel-Poon モデルのパラメータを指定しなければ、自動的に Ebers-Moll のモデルが使用されます。図3に Ebers-Moll の注入モデルを示します。BJTは、2つのpn接合を持っているので、2個のダイオードの組み合わせにより表現できますが、実際にはダイオードを2個接続しただけでは増幅特性が現れません。BJTの増幅現象の本質を手短に述べると、「順バイアスされたB-E接合からベースに注入された少数キャリア(この場合は電子)が、再結合して消滅する前に逆バイアスされたB-C接合に到達してしまうため、ベース中の少数キャリアが、(ベースに電圧を加えたにも関わらず)殆どベース電流とならずに(ベースの多数キャリアと再結合せずに)コレクタへと多量に流れ込んでしまう」ということです。B-C接合が逆バイアスされているだけなら、本来は、僅かに飽和電流が流れるだけなのですが、B-E接合との相互作用により、順バイアスされたB-E接合と同程度の大きな電流がB-C接合に流れてしまうので、両接合の電流の比\(\small I_C/I_E \)(ベース接地電流増幅率)は、ベース内での再結合確率に支配されているため、1より僅かに小さい値となります。電子回路の講義で習うように、高抵抗の逆バイアスpn接合に大きい電流が流れれば、大きな電圧増幅を起こしたことに相当します。さらに、エミッタ接地形式にすれば、下記のように大きな電流増幅率を得ることも可能です。
両接合の電流比であるベース接地電流増幅率を\(\small \alpha_i \)で表すと、
\[ I_C = \alpha_i I_E \tag{2} \]
となります。また、式(1a) を用いて、ベース電流とコレクタ電流の関係を求めると、
\[ I_C = \frac{\alpha_i}{1 – \alpha_i} I_B = \beta_i I_B \tag{3} \]
\(\small \beta_i \)は、ベース電流とコレクタ電流の比\(\small I_C/I_B \)を表し、エミッタ接地電流増幅率と呼ばれます。式(3)より、\(\small \alpha_i = 1 \)ならば、エミッタ接地電流増幅率\(\small \beta_i = 1 \)は、無限大の値となります。このように、図3では、pn 接合 D1 に流れた電流\(\small I_F \)を\(\small A_F \)倍して\(\small I2 \)に流してやることで増幅特性を表現しています。B-E接合への B-C接合の影響も同じように考えることができるので、BJT全体としては、図3下側のように表現することができます。
ここで、\(\small I_F, I_R \)は、pn接合ダイオードに流れる拡散電流なので、ダイオードモデルのページで示したように、下記のような特性を示します。
\begin{eqnarray}
I_F &=& I_{ES} \big( e^{ \frac{q V_{BE}}{kT} } – 1 \big) \tag{4a} \\
I_R &=& I_{CS} \big( e^{ \frac{q V_{BC}}{kT} } – 1\big) \tag{4b}
\end{eqnarray}
式(4a), (4b)を用いて、各端子の電流\(\small I_C, I_E, I_B \)は、下記のように計算されます。
\begin{eqnarray}
I_C &=& A_F I_F \ – I_R \tag{5a} \\
I_E &=& A_R I_R \ – I_F \tag{5b} \\
I_B &=& (1 – A_F) I_F + (1 – A_R) I_R \tag{5c}
\end{eqnarray}
[注] ダイオードモデルのページで説明したように、\(\small GMIN \) (単位 \(\small = \Omega^{-1} \), デフォルト値 \(\small = 10^{-12} \)の値のコンダクタンスが、自動的にpn接合と並列に挿入されます。これは、.OPTIONS コマンドで値を設定できますが、SPICEの計算の収束安定性を確保するためのものなので、\(\small GMIN < 10^{-12} \)にはできません。
このモデルでは、D1, D2の特性を表すパラメータ2個と、増幅特性を表すパラメータ\( A_F, A_R \)の合計4個のデバイスパラメータが必要となります。SPICEでは、パラメータの数を減らした Ebers-Mollの輸送モデルというのが使用されていますので、これについて説明します。
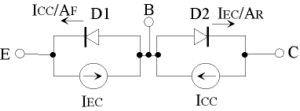
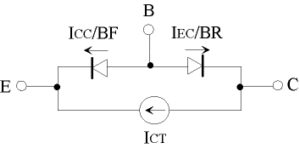
先ず、図4のように変数の置換を行い、電流源を基準とした形に直します。これに伴い、\(\small I_C, I_E, I_B \)は、下記のように書き直されます。
[注] 以後、SPICEのパラメータは、赤文字で示すことにします。
\begin{eqnarray}
I_{CC} &=& A_F I_F = A_F I_{ES} \big( e^{\frac{q V_{BE}}{kT} } – 1 \big) = \textcolor{red}{IS} \big( e^{\frac{q V_{BE}}{kT} } – 1 \big) \tag{6a} \\
I_{EC} &=& A_R I_R = A_R I_{CS} \big( e^{\frac{q V_{BC}}{kT} } – 1 \big) = \textcolor{red}{IS} \big( e^{\frac{q V_{BC}}{kT} } – 1 \big) \tag{6b} \\
I_C &=& I_{CC} \ – \frac{I_{EC}}{A_R} \tag{6c} \\
I_E &=& I_{EC} \ – \frac{I_{CC}}{A_F} \tag{6d} \\
I_B &=& \big( \frac{1}{A_F} – 1 \big) I_{CC} + \big( \frac{1}{A_R} – 1 \big) I_{EC} \tag{6e}
\end{eqnarray}
ただし、
\[ \textcolor{red}{IS} = A_F I_{ES} = A_R I_{CS} \tag{6f} \]
ここまで式を追ってきて、式(6f) または式(6a), (6b)が如何して成立するのか不思議に思われたかもしれません。これを説明するため、先ず電子デバイス等の講義で習った順方向の電流増幅率\(\small A_F \)の大きさを決める物理的パラメータについて復習します。
\[ A_F = A_E A_T A_C \tag{7a} \]
式(7)で、\( A_E \)がエミッタ注入効率で、エミッタ電流のうちベースの少数キャリアによる電流成分の比率です。ベースへの少数キャリア注入のし易さを表し、この値は、エミッタとベースの不純物濃度によって決まります。この値を高くするためには、ベースの不純物濃度をエミッタより低くする必要があります。\( A_T \)がベースの輸送効率で、ベースに注入された少数キャリアが途中で再結合せずにコレクタの接合に到達する比率を表します。この値を高くするためにはベースの厚さが薄い必要があります。\( A_C \)がコレクタ効率で、B-C接合に到いた少数キャリアが、B-C接合の電界でコレクタまで引き出されコレクタ電流になる比率を表します。これは、通常1と近似できます。
\(\small A_C = 1 \)と近似すると、
\[ A_F = A_E A_T = \frac{I_{ne}}{I_F} A_T \tag{7b}\]
ただし、\(\small I_{ne} \)は、B-E接合側のベース領域の少数キャリアの拡散電流成分を表します。
ここで、逆バイアスを印加したB-E接合について考えてみます(図3参照)。逆バイアスによりB-E接合の電流が飽和しているとき、近似的に\(\small I_F = I_{ES} \)が成立します。従って、
\[ A_F = \frac{I_{ne}}{I_F} A_T = \frac{I_{ne}}{I_{ES}} A_T \tag{7c}\]
一方、逆バイアスしたB-C接合でも同様に、
\[ A_R = \frac{I_{nc}}{I_R} A_T = \frac{I_{nc}}{I_{CS}} A_T \tag{7d}\]
\(\small I_{nc} \)は、B-C接合側のベース領域の少数キャリアの拡散電流成分を表します。
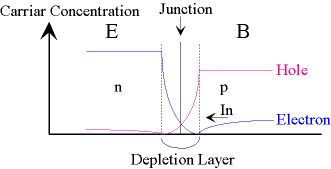
また、図5に示すように、逆方向の拡散電流\(\small I_n \)はベース領域の少数キャリア濃度のみに依存しますので、ベース領域の不純物濃度が均一と仮定すれば、\(\small I_{ne} = I_{nc} \)と考えられます。従って、式(6f)が成立します。
\[ A_F I_{ES} = A_R I_{CS} \tag{6f} \]
式(6a), (5b)により、パラメータを1つ減らすことができたので、Ebers-Moll のモデルを少し簡単化したSPICEのモデルを示します。
\begin{eqnarray}
I_C &=& I_{CC} \ – \frac{I_{EC}}{A_R} \\
&=& \textcolor{red}{IS} \big( e^{ \frac{qV_{BE}}{kT} } – 1 \big) – \frac{ \textcolor{red}{IS} \big( e^{ \frac{qV_{BC}}{kT} } – 1 \big)}{A_R} \\
&=& \textcolor{red}{IS} \big( e^{ \frac{qV_{BE}}{kT} } – e^{ \frac{qV_{BC}}{kT} } \big) – \frac{1 – A_R}{A_R} \textcolor{red}{IS} \big( e^{ \frac{qV_{BC}}{kT} } – 1 \big)
\tag{8}
\end{eqnarray}
ここで、下記のように変数\(\small I_{CT} \)とパラメータ\(\small BR \)を定義します。
\begin{eqnarray}
I_{CT} &=& \textcolor{red}{IS} \big( e^{ \frac{qV_{BE}}{kT} } – e^{ \frac{qV_{BC}}{kT} } \big) \tag{9a} \\
\textcolor{red}{BR} &=& \frac{A_R}{1 – A_R} \tag{9b} \\
I_C &=& I_{CT} \ – \frac{I_{EC}}{\textcolor{red}{BR}} \tag{9c}
\end{eqnarray}
同様に\(\small BF \)を定義すると、次式が得られます。
\begin{eqnarray}
\textcolor{red}{BF} &=& \frac{A_F}{1 – A_F} \tag{9d} \\
I_E &=& I_{EC} \ – \frac{I_{CC}}{A_F} = – I_{CT} \ – \frac{I_{CC}}{\textcolor{red}{BF}} \tag{9e} \\
I_B &=& \frac{I_{CC}}{\textcolor{red}{BF}} + \frac{I_{EC}}{\textcolor{red}{BR}} \tag{9f}
\end{eqnarray}
式(9c), (9e), (9f)より、図6のようなモデルで表現可能であることがわかります。以上の3つのパラメータ、\(\small \textcolor{red}{BF}, \textcolor{red}{BR}, \textcolor{red}{IS} \)がBJTモデルの最も基本的なパラメータとなります。
3.2次的効果の挿入
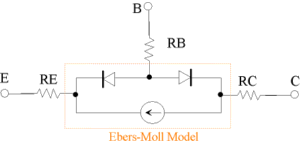
Ebers-Moll モデルは、半導体のpn接合の特性のみを表現しているため、半導体の抵抗とオーミック電極の抵抗を別途挿入する必要があります。図7に各電極に抵抗\(\small \textcolor{red}{RE}, \textcolor{red}{RB}, \textcolor{red}{RC} \)を挿入したモデルを示します。ベース抵抗\(\small \textcolor{red}{RB} \)は、入力側の直列抵抗となるため周波数特性に強力に効くので、値の決定には注意が必要です。エミッタ抵抗\(\small \textcolor{red}{RE} \)は、測定により\(\small \textcolor{red}{RB} \)と見分けることが難しく、次式の形で、ベース抵抗に換算されます。
\[ \textcolor{red}{RB} = (1 + \textcolor{red}{BF}) \textcolor{red}{RE} \tag{10} \]
また、コレクタ抵抗\(\small RC \)は、飽和領域(\(\small V_{CE} \)が小さい)の\(\small I_{C} \ – \ V_{CE} \) 特性の傾きなどに効きます。
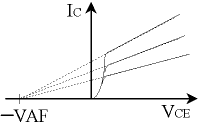
SPICEモデルでは、Early効果をシミュレートするためのアーリ電圧が、パラメータ\(\small \textcolor{red}{VAF} \)として用意されていいます。Early 効果は、電圧\(\small V_{CE} \)を印加するとき、B-C接合の空乏層幅が\(\small V_{CE} \)に依存して変化し、これに伴いベース幅も\(\small V_{CE} \)に依存して変化するため、電流増幅率が\(\small V_{CE} \)により変化してしまう現象です。BJT特性としては、図8のように \(\small I_{C} – V_{CE} \)特性に傾きが現れ、外挿すると、\(\small V_{BE} \)の値によらず、\(\small V_{CE} \)軸と大体1点で交わるという性質があります。ベース幅\(\small W_{B} \)が近似的に\(\small V_{CE} \)と直線関係にあるとすると、次式のように表せます。
\begin{eqnarray}
W_B &=& W_B(0) + \bigg( 1 + \frac{V_{BC}}{\textcolor{red}{VAF}} \bigg) \tag{11a} \\
IS(V_{BC}) &=& \textcolor{red}{IS}(0) \bigg( 1 – \frac{V_{BC}}{\textcolor{red}{VAF}} \bigg) \tag{11b} \\
BF(V_{BC}) &=& \textcolor{red}{BF}(0) \bigg( 1 – \frac{V_{BC}}{\textcolor{red}{VAF}} \bigg) \tag{11c}
\end{eqnarray}
\(\small \textcolor{red}{VAF} \)を定義した場合、SPICEパラメータ\(\small \textcolor{red}{IS}, \textcolor{red}{BF} \)は、式(11b), (11c)の、\(\small \textcolor{red}{IS}(0), \textcolor{red}{BF}(0) \)に相当することに注意してください。また、エミッタとコレクタを入れ替えた逆方向アーリー電圧\(\small \textcolor{red}{VAR} \)というパラメータもあります。
4.蓄積電荷モデル(大振幅特性)
SPICEでは、パルス応答や周波数特性をシミュレーションするために、蓄積電荷モデルに基ずくパラメータが採用されています。このモデルは、パルス回路等の講義で出てきたかもしれませんが、ここで少し復習しておきましょう。半導体内部の少数キャリア分布の時間的変化は、拡散容量の原因となり、またステップ応答の時定数を決定する主要因となります。
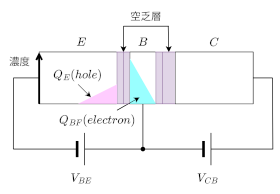
pn接合のバイアスにより注入された少数キャリアの分布が、図9のように直線近似できるとき、キャリアの濃度勾配によって流れる拡散電流は少数キャリアの電荷量に比例すると考えられます。このため、注入された少数キャリアが消えて濃度分布がなくるまで電流が流れ続けるため、BJTの電流をOFFにするためには時間がかかります。
増幅された電流\(\small I_{CC} \)が、電荷\(\small Q_E, Q_{BF} \) に比例し、それぞれの比例係数が\(\small \tau_E, \tau_{BF} \)であったとすると、
\[ Q_E + Q_{BF} = Q_{DE} = ( \tau_E + \tau_{BF} ) I_{CC} \equiv \textcolor{red}{TF} I_{CC} \tag{12a} \]
となります。パラメータ\(\small \textcolor{red}{TF} \)は、トランジェントタイムと呼ばれ、時間の次元を持ちます。
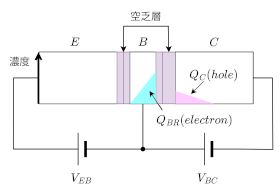
同様に、図10のように電流を流した場合、\(\small I_{EC} \)が、電荷\(\small Q_C, Q_{BR} \) に比例し、それぞれの比例係数が\(\small \tau_C, \tau_{BR} \)であったとすると、
\[ Q_C + Q_{BR} = Q_{DC} = ( \tau_C + \tau_{BR} ) I_{EC} \equiv \textcolor{red}{TR} I_{CC} \tag{12b} \]
となり、パラメータ\(\small \textcolor{red}{TR} \)は、逆方向トランジェントタイムと呼ばれます。
式(12a), (12b) の関係式を用いて、次のようにエミッタ拡散容量\(\small C_{DE} \)とコレクタ拡散容量\(\small C_{DC} \)を計算することができます。
\begin{eqnarray}
C_{DE} &=& \frac{dQ_{DE}}{dV_{BE}} = \textcolor{red}{TF} \frac{dI_{CC}}{dV_{BE}} \tag{13a} \\
C_{DC} &=& \frac{dQ_{DC}}{dV_{BC}} = \textcolor{red}{TR} \frac{dI_{EC}}{dV_{BC}} \tag{13b}
\end{eqnarray}
5.空乏層容量
空乏層内のドナーイオン、アクセプタイオンに対するポアソンの方程式の解より、B-E接合空乏層容量\(\small CJE(V_{BE}) \)、B-E接合空乏層容量\(\small CJC(V_{BC}) \)とC-SUB(半導体基板)間容量\(\small CJS(V_{CS}) \)が次式のように求められます。
\begin{eqnarray}
CJE(V_{BE}) &=& \textcolor{red}{CJE}(0) (1 – \frac{V_{BE}}{\textcolor{red}{VJE}})^{-\textcolor{red}{MJE}} \tag{14a} \\
CJC(V_{BC}) &=& \textcolor{red}{CJC}(0) (1 – \frac{V_{BC}}{\textcolor{red}{VJC}})^{-\textcolor{red}{MJC}} \tag{14b} \\
CJS(V_{CS}) &=& \textcolor{red}{CJS}(0) (1 – \frac{V_{CS}}{\textcolor{red}{VJS}})^{-\textcolor{red}{MJS}} \tag{14c}
\end{eqnarray}
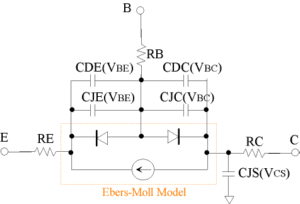
ダイオードモデルのページで説明したように、空乏層容量が順バイアスで発散しないためのパラメータとして、FCが用意されています。値は、0 – 1 の間で適当に設定します。\(\small \textcolor{red}{VJE}, \textcolor{red}{VJC}, \textcolor{red}{VJS} \)はそれぞれの接合のビルトインポテンシャル(pn接合電流-電圧特性の順方向立ち上がり電圧と大体一致)、\(\small \textcolor{red}{MJE}, \textcolor{red}{MJC}, \textcolor{red}{MJS} \)はそれぞれの接合の指数(0.5 – 0.33)で、不純物濃度分布のプロファイルに依存します。以上のモデルを回路図表示すると図11のようになります。
6.Gummel-Poon モデルのパラメータ
Ebers-Mollモデルでは、低電流での電流増幅率低下、ベースの完全空乏層化、高水準注入等が引き起こす特性を表すことができません。Gummel-Poon モデル自体の解説は非常に長くなるので、ここでは幾つかのパラメータの性質について定性的に解説します。
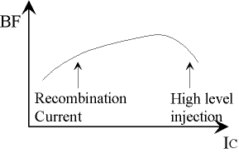
Ebers-MollモデルのBFの\(\small I_C \)依存性\(\small (V_{BC} = const.) \)の概略を図12に示します。 \(\small I_C \)(または\(\small I_B \))が小さい領域と大きい領域で、BFの減少傾向が見られます。\(\small I_C \)の小さい領域では、E-B接合の空乏層での再結合電流が相対的に大きく、エミッタ注入効率が低下しています。また、\(\small I_C \)の大きい領域では、高水準注入により多数キャリアが増加し、やはりエミッタ注入効率が低下します。この様子を\(\small V_{BE} \)を変数とした図13に示します。青い線が\(\small I_B \)、マセンタの線が\(\small I_C \)です。
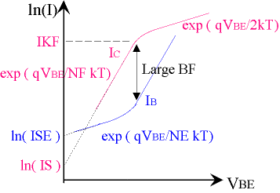
この図の特性を表現するためのパラメータとして次のようなパラメータが使用されています。\(\small \textcolor{red}{NE} \)は、B-E接合リークエミッション係数、\(\small \textcolor{red}{NF} \)は、順方向電流エミッション係数、 \(\small \textcolor{red}{IKF} \)は、順方向大電流BF減少点、\(\small \textcolor{red}{ISE} \)は、B-E接合飽和電流を示しています。逆方向の輸送特性に対しても同様にして、B-C接合リークエミッション係数\(\small \textcolor{red}{NC} \)、逆方向電流エミッション係数\(\small \textcolor{red}{NR} \)、逆方向大電流BF減少点\(\small \textcolor{red}{IKR} \)、B-C接合リーク飽和電流\(\small \textcolor{red}{ISC} \)が定義されます。この他、内部ベース抵抗(エミッタ直下の領域)の\(\small I_B \)依存性や、\(\small TF \)のバイアス依存性、各種温度依存性やノイズ特性などを決定するパラメータ(ダイオードモデルのページ参照)が準備されていますが、ここでは省略します。
以上のSPICEパラメータをまとめると次の表のようになります。
| パラメータ | 意味 | デフォルト値 | 単位 | 備考 |
|---|---|---|---|---|
| IS | 飽和電流 | \( 10^{-16} \) | A | 面積ファクタの影響有り |
| BF | 最大順方向増幅率 | 100 | ||
| BR | 最大逆方向増幅率 | 1 | ||
| RB | ベース抵抗 | 0 | \( \Omega \) | 面積ファクタの影響有り |
| RE | エミッタ抵抗 | 0 | \( \Omega \) | 面積ファクタの影響有り |
| RC | コレクタ抵抗 | 0 | \( \Omega \) | 面積ファクタの影響有り |
| VAF | 順方向アーリ電圧 | \( \infty \) | V | |
| VAR | 逆方向アーリ電圧 | \( \infty \) | V | |
| TF | 順方向トランジェントタイム | 0 | s | |
| TR | 逆方向トランジェントタイム | 0 | s | |
| CJE | ゼロバイアスB-E接合容量 | 0 | F | 面積ファクタの影響有り |
| CJC | ゼロバイアスB-C接合容量 | 0 | F | 面積ファクタの影響有り |
| CJS | ゼロバイアスC-S接合容量 | 0 | F | 面積ファクタの影響有り |
| VJE | B-E接合ビルトイン電圧 | 0.75 | V | |
| VJC | B-C接合ビルトイン電圧 | 0.75 | V | |
| VJS | C-基板接合ビルトイン電圧 | 0.75 | V | |
| MJE | B-E接合C-V特性指数 | 0.33 | ||
| MJC | B-C接合C-V特性指数 | 0.33 | ||
| MJS | C-基板接合C-V特性指数 | 0 | ||
| FC | 順方向バイアス空乏層容量係数 | 0.5 | ||
| NE | B-E接合リークエミッション係数 | 1.5 | ||
| NC | B-C接合リークエミッション係数 | 2 | ||
| NF | 順方向電流エミッション係数 | 1 | ||
| NR | 逆方向電流エミッション係数 | 1 | ||
| IKF | 順方向大電流BF減少点 | \( \infty \) | A | |
| IKR | 逆方向大電流BF減少点 | \( \infty \) | A | |
| ISE | B-E接合リーク飽和電流 | 0 | A | |
| ISC | B-C接合リーク飽和電流 | 0 | A | |
| EG | バンドギャップ | 1.11 | eV | |
| XTI | ISの温度べき乗指数 | 3 |
演習問題
Ebers-Mollモデルのパラメータ\(\small BF, BR, IS \)の値が、BJTの特性にどのような影響を与えるか調べるため、B-E接合順バイアス、B-C接合逆バイアスの条件下で、電子回路シミュレーションを実施して、下記のグラフを作成しましょう。ただし、\(\small BF = 10 \sim 1000, BR = 10 \sim 1000, IS = 10^{-16}A \)とする。
- \(\small \ln I_C \ – V_{BE} \)プロット
- \(\small \ln I_B \ – V_{BC} \)プロット
