演算増幅器の特性は、電子回路シミュレータのAC解析によって容易に得られますが、実測するためには少し工夫が必要です。特別な計測器は必要ありませんが、専用の測定回路を製作する必要があります。工学部の学生実験等で学ぶ内容ですが、電子情報通信学系でも意外と知らない人が多いので、学生向けの解説として残しておきます。
例えば、入力換算オフセット電圧\(\small V_{OS} = 1mV \)、差動利得\(\small A_d = 120dB = 1,000,000 \)の演算増幅回路の+/-入力をショートした場合、計算上は出力に1000Vの電圧が発生することになります。市販のシングルエンド演算増幅器は、コモンモードフィードバックがないため、負帰還をかけない状態で、+/-入力をショートすると、微小なオフセット電圧の正負に応じて、出力電圧がVDDまたはVSSに飽和した状態となり、オープンループ利得は測定できません。
オフセット電圧の測定
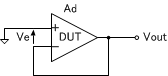
上図の回路の様に、負帰還をかけて、1倍の正相増幅器(ボルテージフォロワ)にしてみると下の式のように、\(\small V_{out} \)から、オフセット電圧\(\small V_{OS} \)を求めることができます。この回路の動作原理は、次のとおりです。
\begin{cases}
V_{out} &=& – V_e \\
V_{out} &=& A_d ( V_e \ – \ V_{OS} )
\end{cases}
\[ V_{out} = A_d ( V_e \ – \ V_{OS} ) \]
\[ V_{out} = A_d ( – V_{out} \ – \ V_{OS} ) \]
\[ V_{out} = – \frac{A_d}{1 + A_d} V_{OS} \xrightarrow{A_d \gg 1} V_{out} = – V_{OS} \]
この測定では、電源の+/-の値も、なるべく正確に大きさを合わせておきます。差動増幅器は、2つの入力の差をとるため、電源電圧が変わっても相殺されるため電源電圧の影響は受けません(同相入力成分のキャンセル)。しかし、実際には、同相入力除去は完全ではないため、測定結果が電源電圧の影響を受けます。特にシングルエンド演算増幅器のシステマティックオフセットは、電源電圧の影響を受けます。
オフセット電圧は、通常 1mV以下なので、ナノボルトメータまたは高精度マルチメータを持っていれば測定できますが、シールドや積分時間の設定など、それなりに注意が必要です。これを回避するためには、ボルテージフォロワの代わりに、正相増幅回路を構成し、利得を持たせる方法が考えられます。しかし、DUTに利得を持たせると、その分、仮想ショート(Virtual short)の精度が落ちるため( \(\small A_d \ne \infty \))、測定精度も下がります。
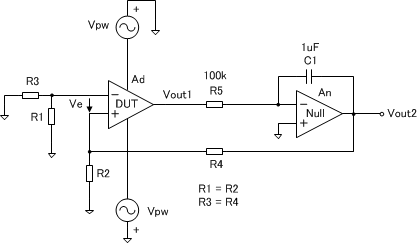
そこで、通常は、下記のような補助アンプ(Nullアンプとも呼ばれる)を介して負帰還をかけ、DUT自体はオープンループ動作させ、Nullアンプに正確な\(\small V_{OS} \)キャンセル電圧を出力させます。Nullアンプは、積分器を構成しており、直流で大きな利得( = DCゲイン)を持つため、\(\small V_{OS} \)をキャンセルするために必要な\(\small V_e \)をDUTに印加すると同時に、\(\small V_e \)を与えるのに必要な電圧値を\(\small V_{out2} \)に出力します。従って、\(\small V_{out2} \)の一部(\(\small R2 \)と\(\small R4 \)で分圧)をDUTに負帰還させるようにすれば、\(\small V_{OS} \)を\(\small 1 + R4/R2 \)倍に拡大した電圧を\(\small Vout2 \)に出力させることができます。Nullアンプは、単に利得の大きい増幅器であればよいため、とくに高い性能は要求されませんが、DUTと同じものを使用しておけば安全です。また、Nullアンプの入力レンジを大きくとるため、Nullアンプの電源電圧は、DUTの電源電圧と同じか、それよりも大きくします。
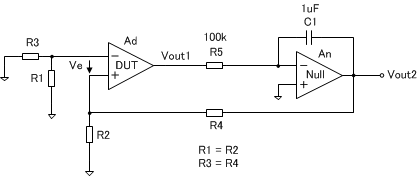
\begin{cases}
V_{out1} &=& A_d ( V_e \ – \ V_{OS1} ) \\
V_{out2} &=& A_n ( – \ V_{out1} \ – \ V_{OS2} ) \\
V_e &=& \dfrac{R2}{R2 + R4} V_{out2}
\end{cases}
上記回路方程式から、\(\small V_{out2} \)と\(\small V_{OS1} \)の関係が求められます。
\[V_{out2} = \frac{1}{ \dfrac{1}{A_n A_d} + \dfrac{R2}{R2 + R4} } V_{OS1} – \frac{1}{A_d} \frac{1}{ \dfrac{1}{A_n A_d} + \dfrac{R2}{R2 + R4} } V_{OS2} \]
\[\xrightarrow{A_n A_d \gg 1} \bigg( 1 + \frac{R4}{R2} \bigg) V_{OS1} – \frac{1}{A_d} \bigg( 1 + \frac{R4}{R2} \bigg) V_{OS2} \]
\[\xrightarrow{A_d \gg 1} \bigg( 1 + \frac{R4}{R2} \bigg) V_{OS1}\]
\(\small V_{out2} \)を \(\small 1/(1 + R4/R2) \)倍に縮小したときに、\(\small V_{OS1} \)を相殺するように \(\small V_{out2} \)が制御されることがわかります。また、Nullアンプのオフセットは、DUTの利得が大きければ無視できることも分かります。
この式を用いて、例えば、R1 = R2 = 100, R3 = R4 = 99.9k とすると、\(\small V_{out2} = 1000V_{OS} \) となり、1mV以下のオフセット電圧が容易に測定できます。ただし、抵抗器には、十分な精度は無いので、事前に正確な抵抗値を測定しておく必要があります。
DCオープンループ利得の測定
演算増幅回路の性能は、差動利得ではなく、GBP(利得帯域幅積)で決まりますが、計測回路やADCの場合は、DC付近での有効桁数を保証するために、DC差動利得を知りたい場合がよくあります。高性能演算増幅器のDCオープンループ利得は、120dB~140dB以上にもなります。例えば、120dB(1,000,000倍)の演算増幅器の出力電圧が1Vのとき、入力電圧は1uVとなります。高級な電源や信号源でも、これだけ低雑音、低ドリフトのものはありません。ここでも、Nullアンプを使用した測定回路を用います。Nullアンプは、DUTのオフセット電圧を負帰還により相殺すると同時に、DUTの出力電圧に対して、必要な入力電圧を正確にDUTに印加する目的で使用されています。言葉では、分かりにくいと思いますが、式を追ってみると簡単です。
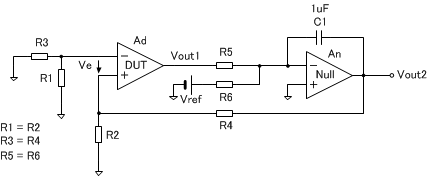
式が複雑になるので、ここでは、\(\small V_{OS1} \)は無視することにし、\(\small V_{ref} \gg V_{OS2} \) となるように \(\small V_{ref} \) を与えます。
\begin{cases}
V_{out1} &=& A_d V_e \\
V_{out2} &=& – A_n \dfrac{V_{out1} \ – \ V_{ref}}{2} \\
V_e &=& \dfrac{R2}{R2 + R4} V_{out2}
\end{cases}
回路方程式より、\(\small A_d \)と\(\small V_{out2} \)の関係を求めると以下のようになります。
\[ A_d = \frac{V_{out1}}{V_e} = \frac{ -\dfrac{2}{A_n} V_{out2} + V_{ref} }{ \dfrac{R2}{R2 + R4} V_{out2}} \xrightarrow{A_n \gg 2} \bigg( 1 + \frac{R4}{R2} \bigg) \frac{V_{ref}}{V_{out2}} \]
適当な、\(\small V_{ref} \)を与え、\(\small V_{out2} \)を測定すれば、DC利得を求めることができます。例えば、R1 = R2 = 100, R3 = R4 = 99.9k, R5 = R6 = 200k, Vref = 1V 辺りでしょうか。
ACオープンループ利得の測定
DC利得の測定で用いた\(\small V_{ref} \)を用いてAC特性を測定しようとすると、Nullアンプの積分特性の影響を受けるため、DUTの周波数特性が求められません。そこで、Nullアンプは、\(\small V_{OS} \)のキャンセルのためだけに使用し、AC信号をDUTに直接入力し、\(\small V_{out1} \)を測定することにします。しかし、前節で述べたように、微小で低ノイズの信号源を用意することは難しいので、ある程度周波数が高くなり(数100~1kHzぐらい?)、オープンループ利得が下がったところを測定します。低周波の部分は、測定できた周波数特性を外挿して。DC利得と交わるところが、ポールの周波数です。R1 = R2 = 100, R3, R4 = 99.0k ぐらいで。出力波形が綺麗に出なければ、R3を大きくするか、\(\small v_{sig} \) の振幅を小さくしてみます。
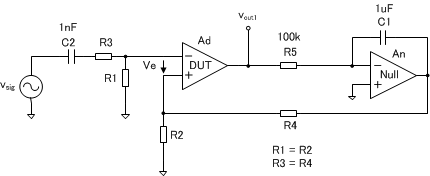
\[ |A_d(\omega)| = \frac{|V_{out1}|}{|V_e|} = \frac{|V_{out1}|}{\dfrac{R1}{R1 + R3}|v_{sig}|} = \bigg( 1 + \frac{R3}{R1} \bigg) \frac{|V_{out1}|}{|v_{sig}|} \]
CMRRとPSRRの測定
オフセット測定回路で、同相入力を行う代わりに、電源電圧を変化させて、等価的に同相入力を行います。このため、正負電源電圧のトータルが変わらないようにし、相対的にGNDレベル(VDDとVSSの平均値)だけが変わるようにします。
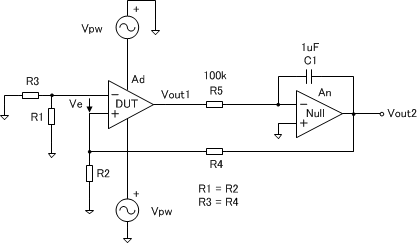
\[ CMRR = \frac{A_d}{A_c} = \frac{ \dfrac{dV_{out1}}{dV_{diff}} }{ \dfrac{dV_{out1}}{dV_{com}} } = \frac{dV_{com}}{dV_{diff}} = \frac{dV_{pw}}{dV_{out2}} \]
PSRRの測定の場合は、正負電源電圧のトータルだけを変化させ、GNDレベルが変わらないようにします。