回路の動作速度は、負荷容量によって変化するため、回路設計の前に、使用する素子の寄生容量や負荷となる回路の入力容量の値を知っておく必要があります。また、LC共振VCOでは、MOSFETのゲート容量やpn接合容量で発振周波数レンジを決定します。半導体デバイスや電子回路の容量は、通常のキャパシタとは異なり、DC電圧によって値が変化するため、DC電圧を変数とした下記の小信号容量\(\small C(V)\)として定義されます。
\[ C(V) = \frac{dQ}{dV} = \frac{i}{\dfrac{dV}{dt}} \]
市販のC-Vメータには、測定レンジや測定周波数によって、いろいろな方式の測定回路が使われていますが、電子回路シミュレータの場合は、測定対象デバイス(DUT)に対して、小信号電圧を加え、電流の実部と虚部を測定すれば、小信号容量を算出できます。
AC解析による小信号容量の計算法
キャパシタンスのリーク電流が無視できる場合、DUTの小信号等価回路は、下図のようなCR直列回路で表せます。
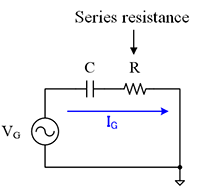
この回路方程式を、電流\(\small I_G \)の実部と虚部で表すと次のようになります。
\[
\let\Re\relax
\DeclareMathOperator{\Re}{Re}
\let\Im\relax
\DeclareMathOperator{\Im}{Im}
V_G = \bigg( \frac{1}{j \omega C} + R \bigg) [ \Re (I_G) + j \Im (I_G) ]
\]
小信号\(\small V_G \)の振幅\(\small = 1V\), 位相\(\small = 0\)とするとき、以下の式(1), (2)が成り立つため、\(\small R\)と\(\small C\)を求めることができます。
\[
\let\Re\relax
\DeclareMathOperator{\Re}{Re}
\let\Im\relax
\DeclareMathOperator{\Im}{Im}
\Re (V_G) = R \Re (I_G) + \frac{\Im (I_G)}{\omega C} = 1 \tag{1}
\]
\[
\let\Re\relax
\DeclareMathOperator{\Re}{Re}
\let\Im\relax
\DeclareMathOperator{\Im}{Im}
\Im (V_G) = R \Im (I_G) \ – \ \frac{\Re (I_G)}{\omega C} = 0 \tag{2}
\]
\[
\let\Re\relax
\DeclareMathOperator{\Re}{Re}
\let\Im\relax
\DeclareMathOperator{\Im}{Im}
C = \frac{\Im (I_G)}{\omega} \bigg( 1 + \frac{\Re (I_G)^2}{\Im (I_G)^2} \bigg) \tag{From Eq.(1)}
\]
\[
\let\Re\relax
\DeclareMathOperator{\Re}{Re}
\let\Im\relax
\DeclareMathOperator{\Im}{Im}
R = \frac{\Re (I_G)}{\Im (I_G)} \frac{1}{\omega C} \tag{From Eq.(2)}
\]
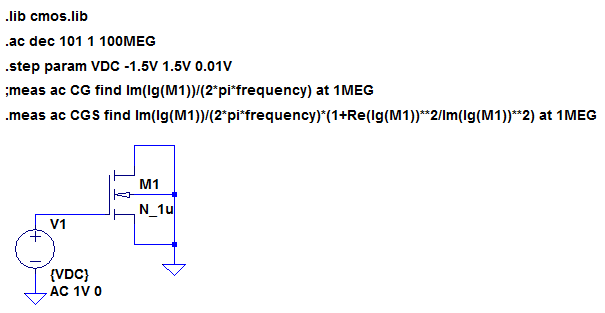
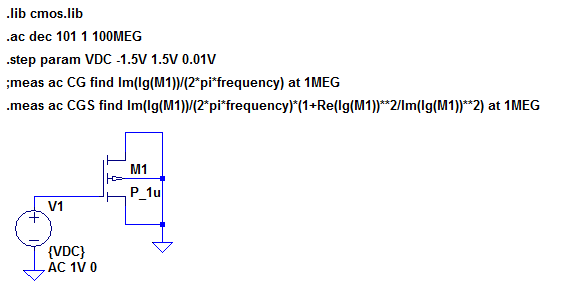
MOSFETのC-V特性測定例
n-ch および p-ch MOSFETのゲート-ソース/ドレイン間容量の測定回路例を次に示します。測定周波数は、1MHz、直流電圧は、-1.5V~+1.5V としています。